Aufgabe A 1.1
 Der Graph der Funktion f mit
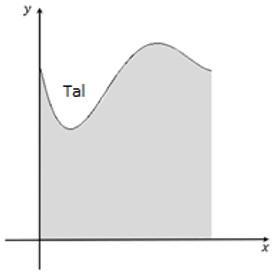
Der Graph der Funktion f mit
f(x)=0,3x4-2,8x3+8,3x2-7,6x+6
beschreibt modellhaft für 0≤x≤3,8 das Profil eines Geländequerschnitts (siehe Abbildung).Die positive x-Achse weist nach Osten und f(x) gibt die Höhe über dem Meeresspiegel an (eine Längeneinheit entspricht 100 Meter).
Eine Brücke führt in West-Ost-Richtung auf einer konstanten Höhe von 500 Meter über dem Meeres- spiegel über das Tal.
a) Berechnen Sie den Höhenunterschied zwischen dem höchsten und dem tiefsten Punkt des Profils.
Bestimmen Sie die Stelle, an der das Gelände am steilsten ist.
Bestimmen Sie die Länge der Brücke.
Ermitteln Sie die durchschnittliche Steigung des Geländeprofils zwischen dem östlichen Ende der Brücke und dem höchsten Punkt des Profils.
(5 VP)
b) An einem Punkt der Brücke, der im Modell die Koordinaten P(1|5) hat, wird ein 30 Meter langes Seil befestigt, das senkrecht nach unten hängt.
Das untere Ende des Seils soll zu jedem Punkt des Geländeprofils einen Mindestabstand von 15 Meter haben.
Untersuchen Sie, ob dieser Mindestabstand eingehalten wird.
(3 VP)
c) Eine Drohne steigt vertikal von einer Position auf, die durch den Punkt D(2,5|f(2,5)) dargestellt wird. Die Drohne verfügt über eine Kamera.
Ermitteln Sie, ab welcher Höhe über dem Gelände die Kamera den Ort auf der Brücker erfassen kann, der durch den Punkt P(1|5) dargestellt wird.
(4 VP)
d) Bei der Schneeschmelze füllt sich das Tal mit Wasser. Dabei entsteht ein See, der Im Querschnitt 30 Meter breit ist.
Berechnen Sie die durchschnittliche Tiefe der Querschnittsfläche des Sees.
(3,5 VP)
Aufgabe A 1.2
Für jede reelle Zahl k ist eine Funktion fk(x)=k·ex-2x·ex gegeben.
a) Bestimmen Sie die Nullstellen von fk.
(1 VP)
b) Zeigen Sie, dass f(k+2) eine Stammfunktion von fk ist.Der Graph von f2 schließt mit der positiven Koordinatenachse eine Fläche ein.
Bestimmen Sie ihren Inhalt exakt.
(3,5 VP)
| Downloads |
PowerPoint